«Новый» подход к рекурсии?

Question

[denny_cat]

Вопрос возник в связи с реализацией известной функции Хофштадтера на Питоне
с использованием мемоизации. Но можно начать и с обычных чисел Фибоначчи.
Определим:
F(n) = F(n-1) + F(n-2)
Что не так в этом определении? Здесь нет начальных условий!
Получается, мы начинаем с пустого словаря memo_dict = {}
И если начать с n = 1, то первый же запрос F(n-1) выдаст ошибку KeyError.

Да, но у нас же есть перегрузка методов! Перепишем __missing__так, чтобы при запросе на несуществующий ключ не выдавалась ошибка, а ему присваивалось бы определенное default значение, скажем 1.
Таким образом, первое обращение к функции потребует принудительного добавления в словарь {-1: 1, 0: 1}
Рекурсия в некотором смысле «нырнет в неизвестное», но потом все продолжится естественным образом! Вычисление каждого нового значения будет использовать уже созданный словарь. Глубина «погружения» в неопределенность окажется равной 2.

Теперь обратимся к QHofstadter
Q(n) = Q(n - Q(n-1)) + Q(n - Q(n-2))

Начав с пустого словаря, n = 3 и default = 1, все произойдет также, как и для Фибоначчи:
возникнут классические начальные условия {1: 1, 2: 1} и далее все по плану.

Мне очень любопытно, есть ли какие-то статьи и исследования о таком подходе к рекурсии?

То, что он не тривиален, легко убедится на примере той же QHofstadter.
Начнем со словаря {1: 2, 2: 1}. На третьем шаге рекурсия «нырнет» к неопределенному ключу 0, но потом опять пойдет вперед самостоятельно. Пробуя другие, небольшие целочисленные начальные значения, мы увидим самые разнообразные примеры «погружения в неизвестное»:

{1: 5, 2: 6}

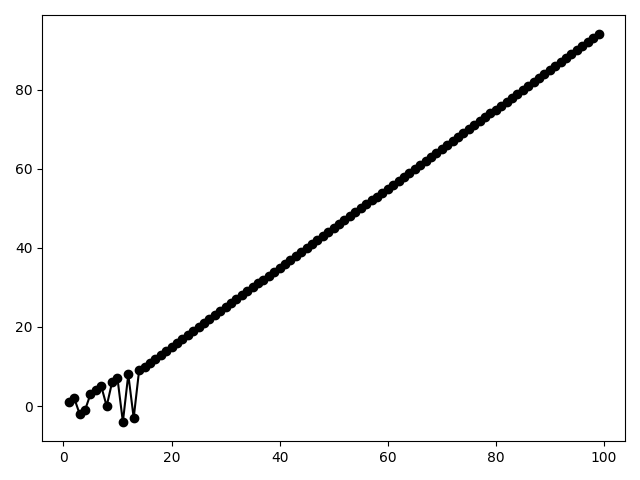{1: 4, 2: 5}

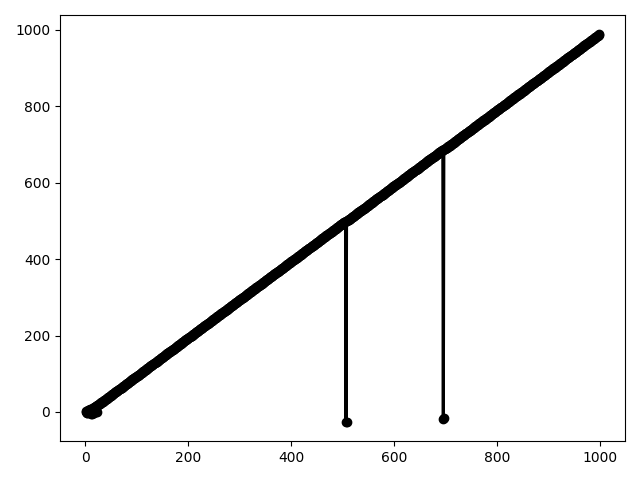{1: 8, 2: 3}


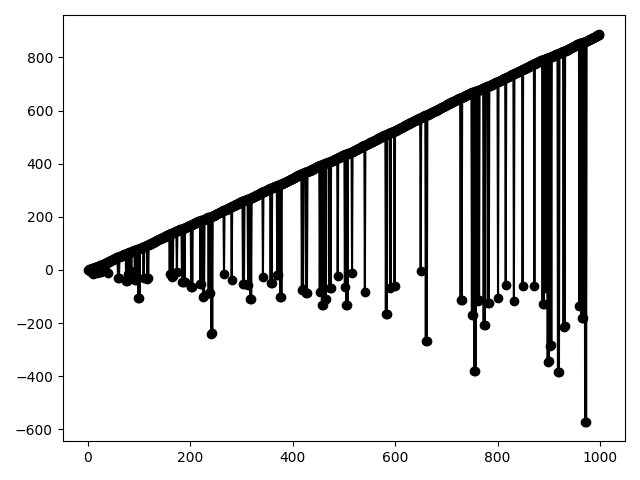
Мне бы хотелось продолжить исследования, но возможно, эта тема уже давно раскрыта.
Буду признателен за любые комментарии и ссылки!

Comments

[Алан Гибизов]

Вы немного перепутали - это не сюда надо писать. См.п.3.4 Правил
Тема интересная, но тут не место для обсуждения таких тем. Тут не форум и не соцсеть. Это вопросы и ответы.

Answer 1

[dollar]

Нет, подход не «новый».

Автор, дам советы по изложению больших текстов (не литературных, а по делу).

• Название не должно содержать интригу, а быть максимально понятным.
  
• В первом абзаце должно быть вступление, которое ещё детальнее раскрывает тему и объясняет, что будет дальше (но не частично, а полностью). Не нужно начинать издалека. Это просто обобщение, абстрактный уровень того, что будет дальше. То есть нужно начать с главного, с объяснения сути.
  
• В последнем абзаце примерно то же самое, что и в первом, то есть тоже обобщение, только с позиции завершения (с позиции выводов).
  
• И с учётом специфики этого ресурса, среднюю часть лучше вообще загнать под спойлер, если там больше 2 абзацев. Большие статьи лучше вообще в другом месте публиковать, но порядок изложения тот же нужен будет.
  

Comments

[denny_cat]

Нет, подход не «новый».

Что можно посмотреть на эту тему?

[shurshur]

denny_cat, в реальном программировании никто не делает рекуррентные функции, которые не содержат начальных условий. Поэтому вопрос вообще непонятен, причём тут "новый подход"? Ну, например, функция fib для начальных значений будет возвращать результат явно, а не рекурсивным вызовом:

def fib(n:int):
    assert n>=0
    if n < 2: return 1
    return fib(n-1)+fib(n-2)

Answer 2

[Akina]

Что-то уж больно на бред воспалённого сознания похоже.

В любом, абсолютно любом рекурсивном алгоритме есть условия завершения рекурсии, при которых алгоритм возвращает специальное заранее статически заданное значение.

Но можно начать и с обычных чисел Фибоначчи.

В случае рекурсивной реализации ряда Фибоначчи это условие n<2 и специальное значение 1. Смешно, но совершенно такие же и условие, и спецзначение у Хофштадтера.