Я занимаюсь научными расчетами, и внезапно обнаружил очень странный эффект. Если вызывать интеловский (встроенный в Intel Fortran) генератор равномерно распределенных случайных чисел (0,1)
много раз подряд, то на
некоторых компах он
изредка возвращает NaN.
UPD: И еще три важных нюанса:
1) Чуть позже я обнаружил, что совершенно аналогичный гейзенбаг возникает при преобразовании 64-битного целого в 64-битное число с плавающей точкой.
Некоторые подробности здесь.
2) Для возникновения бага необходимо, чтобы где-то в программе был еще и запрос системного времени. Причем обязательно из другого модуля (который компилируется отдельно)!
3) Баг возникает, только если собирать программу c полной оптимизацией. У меня в фортране это ключи /MP /O2 /QaxSSE3 /QxSSE3 /Qparallel. При сборке без оптимизации результат будет NaN-free.
Теперь подробнее.
1. Про оптимизацию
Зависимость бага от настроек оптимизации меня, мягко говоря, удивила, так как генератор случайных чисел, по идее, должен в обоих случаях вызываться один и тот же. Поскольку функция RANDOM цепляется из какой-то стандартной библиотеки, я полез в дизассемблер, чтобы понять разницу между двумя версиями ГСЧ (сборка с оптимизацией и без нее). Сам генератор, как и следовало ожидать, действительно в обоих случаях одинаковый. Но внутри кода RANDOM есть
один внешний вызов
Для начала предупреждаю, что в ассемблере я ни бум-бум, и пишу только на фортране! Поэтому все написанное под этим спойлером может оказаться полным бредом и воспаленным воображением. Я всего лишь хотел собрать хоть какую-то информацию про обнаруженный баг.
Итак, я дизассемблировал две версии своей тестовой программы: с ключом оптимизации /Od (оптимизация запрещена) и /O2 (оптимизация скорости). Оказалась, что сама функция-генератор случайных чисел в двух версиях идентична (с точностью до ее расположения в памяти, но это понятно).
Однако, внутри этой функции есть один внешний вызов:
005C052B call _for__acquire_semaphore_threaded (596C80h)
Внутри которого (после череды других call) происходит что-то уже совсем-совсем для меня непонятное:
75C34043 call 75C443C5
(...)
75C443C5 jmp dword ptr ds:[75BA007Ch]
Для непосвященного это напоминает call по адресу, хранящемуся в ячейке памяти (указатель на функцию?). Как такое дебажить, особенно если нештатное срабатывание может первый раз произойти через 50 млн вызовов, я себе представляю плохо. Точнее, не представляю вообще: это вопрос совершенно не моего уровня компетенций :-((
Но на всякий случай добавлю, что программа у меня однопоточная и, по идее, ничего согласовывать с другими потоками не должна. С другой стороны, в языке есть массивные операции, которые могут распараллеливаться автоматически, и, теоретически, генератор случайных чисел может в этом случае как-то донастраиваться для параллельных вычислений. В справке я об этом ничего не нашел, но это может быть не проблемой справки, а моей личной проблемой (справка написана по-английски, а у меня отношения с ним не сложились :-(.
2. Про детерминированность бага:
Благодаря наводящему вопросу
Tony, хочу уточнить один важный нюанс: даже при генерации
одинаковых последовательностей ПСЧ (инициализация SEED одной и той же константой) NAN-ы при каждом запуске появляются в
разных местах.
UPD: вот подробности (картинка с результатами теста)
На этой картинке три ряда.
Первый и второй ряды (зеленый и желтый) - две это последовательности нормально распределенных ПСЧ, полученные при двух запусках тестовой программы с одинаковым SEED(301). Каждое значение сигнала на графике - это сумма 12-ти значений RANDOM минус 6. Тем самым я получаю нормально распределенное случайное число, а заодно уменьшаю длину ряда в 12 раз. Если хотя бы один из 12-ти вызовов RANDOM вернул NaN, то и значение Noise на графике тоже будет NaN. Таким образом, чтобы получить 1 000 000 значений Noise, я вызываю функцию RANDOM 12 млн раз.
Третий ряд (синий) - это разность между первым и вторым рядом.
NaN-ы, как и на всех остальных картинках, закодированы числом 99. Соответственно, разность двух первых рядов дает либо 0 (если значения совпадают), либо +-99 (примерно).
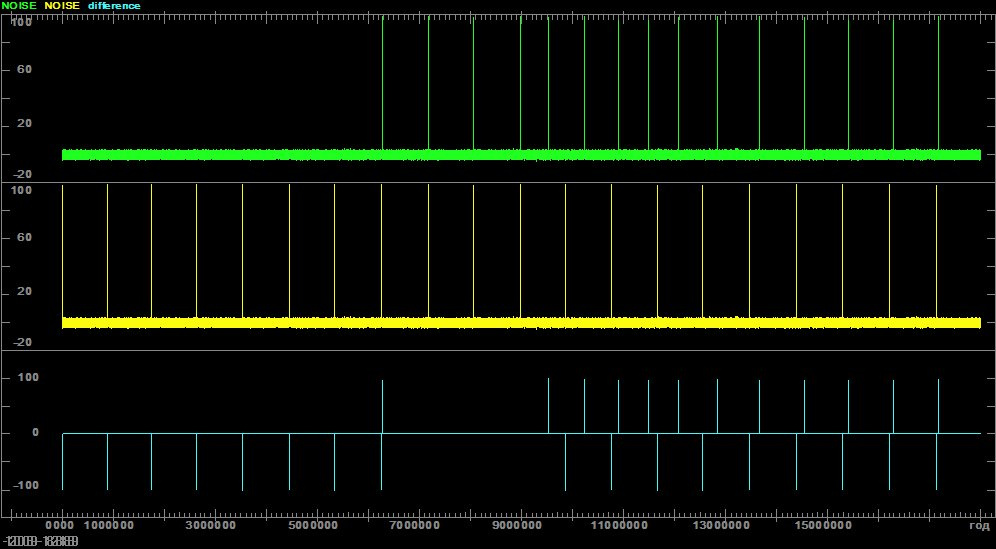
Из картинки видно, что NaN-ы появляются:
а) редко,
б) в случайные моменты времени, и
в) эти моменты времени меняются от запуска к запуску, даже если ГСЧ инициализирован одним и тем же числом, и последовательности ПСЧ одинаковые.
За исключением NaN-ов...
И еще интересный нюанс. На участке от 6.3 до 9.5 млн NaN-ы в двух последовательностях ПСЧ в точности совпадают! Напомню, что между последовательными NaN-ами примерно по 0.8 млн вызовов Noise, или около 10 млн вызовов RANDOM. То есть, вероятность случайного совпадения двух NaN-ов в рядах Noise примерно E-6. А в приведенном примере они совпали трижды подряд!
Однако, после совпадения трех NaN-ов подряд следующие NaN-ы (на отметке 9 500 000) в двух тестах разные! И дальше последовательности расходятся.
Анализ этой и других подобных картинок показывает, что:
1) Момент появления первого NaN в последовательности ПСЧ как-то зависит от того, чем инициализирован ГСЧ.
2) Появление NaN зависит как от внутренних переменных ГСЧ (иначе мы бы никогда не увидели точное совпадение NaN в двух разных последовательностях), так и еще от каких-то внешних по отношению к ГСЧ факторов (иначе бы при одинаковом внутреннем состоянии ГСЧ NaN всегда появлялись бы в одинаковые моменты времени).
-------------
Будет ли аналогичный эффект наблюдаться в других языках/компиляторах, я проверить не могу, но подозреваю, что у фортрана и Си базовые математические библиотеки часто общие. Даже название функции - RANDOM в современном фортране и Си одинаковое. А другие языки могут что-то таскать из Си-шных библиотек.
-----------
Для себя я пока сделал подпорку: обернул встроенный генератор случайных чисел в свою функцию, которая в случае isNan(Random) вызывает генератор повторно. И аналогично сделал с преобразованием Real*8 = Integer*8. Но это решение суррогатное, т.к. этот же баг иногда появляется и в других ситуациях, а также при вызове встроенных функций. Поэтому хочется все же понять причину бага, а заодно и предупредить о нем других "заинтересованных лиц".
UPD: к сожалению, я столкнулся с ограничением на длину вопроса (не более 10 000 знаков, поэтому более полную информацию про баг, включая ассемблерный код в двух вариантах, описание ключа /О2 в справке фортрана и др., вынужден вынести в отдельный Word-файл:
FORTRAN_URAND_BUG.doc
Там же приведен исходный фортрановский код, а также дана ссылка на скачивание моего exe-шника с тестом. Если будет не влом - запустите его на своем процессоре и напишите мне, что получилось. Только не забудьте при сборке теста про оптимизацию: без нее никаких глюков не будет (но это не точно ;-)
И еще одна версия о причинах бага
Глядя на битовые маски:
Random == 11111111110000000000000000000000 // NaN
R=1.00 == 00111111100000000000000000000000 // 1.00000
возникает подозрение, что проблема может возникать на этапе преобразования int -->> real. Насколько я понимаю, исходный алгоритм генератора псевдослучайных чисел обычно работает с integer. Более того, он никогда не дает числа вида 00000000 или FFFFFFFF. Поэтому на выходе фортран-генератора не должно быть ни точных 0, ни точных 1.000. Но как известно, точность представления чисел с плавающей запятой ограничена. Около 0 это не влияет, а вот вблизи 1 некоторые integer-ы могут преобразовываться в R=1.000
С другой стороны, если бы это было именно так, то это преобразование работало бы одинаково с оптимизацией и без нее (или нет?).
В общем, если вы заинтересуетесь и попробуете вызвать RANDOM из Си, то включайте максимальную оптимизацию: бажит только оптимизированная программа. Правда, я не очень понимаю, можно ли включить в Си многопоточность одним ключом /MP, или надо специально цеплять для этого всякие либы. В фортране-то параллельность заложена в языке (массивные операторы) и от пользователя не требуется много ума, чтобы ее подключить...
====================
UPD-2023: Спустя год вновь возникла необходимость вернуться к вопросу, и я с удивлением обнаружил, что мой ответ на вопросы
thecove куда-то пропал... Как и вообще вся дискуссия (если мне не изменяет память, тут была целая ветка обсуждений). Поэтому отвечаю заново еще раз, но уже в тексте основного вопроса, чтобы мой ответ опять не пропал:
----------------------------
...Rand в фортране выдает число типа float / double?
Да
Если написать простую голую программу в которой будет только один вызов функции Rand в цикле и больше ничего. NaN - появляется???
Нет.
Где-то в программе обязательно должен быть еще и запрос системного времени, причем обязательно из другого модуля (который компилируется отдельно).
PS можете приложить асм листинг функции Rand ?
Дизассемблер добавлен в тот же самый файл:
FORTRAN_URAND_BUG.doc 