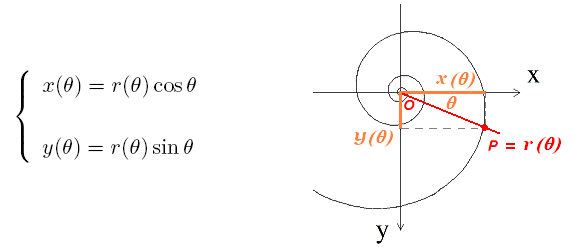
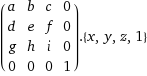Можно умножить получаемые координаты на нужную матрицу трансформации.
https://habr.com/ru/post/319144/ раздел "Матрица вращения"
Матрица считается один раз перед рисовкой, а потом все координаты спирали умножаются на неё.
Пример:
Есть у нас вектор, вокруг которого хотим повернуть всю спираль: (vx,vy,vz)
Есть угол, на который хотим повернуть: a
Тогда матрица поворота вокруг этого вектора выглядит так:
{
{cos(a)+(1-cos(a))*vx*vx, (1-cos(a))*vx*vy-sin(a)*vz, (1-cos(a))*vx*vz+sin(a)*vy, 0},
{(1-cos(a))*vy*vx+sin(a)*vz, cos(a)+(1-cos(a))*vy*vy, (1-cos(a))*vy*vz-sin(a)*vx, 0},
{(1-cos(a))*vz*vx-sin(a)*vy, (a-cos(a))*vz*vy+sin(a)*vx, cos(a)+(1-cos(a))*vz*vz, 0},
{0, 0, 0, 1}
}
Чтобы упростить формулы, обозначу элементы матрицы через переменные a,b,c,d,e,f,g,h,i
a=cos(a)+(1-cos(a))*vx*vx
b=(1-cos(a))*vx*vy-sin(a)*vz
c=(1-cos(a))*vx*vz+sin(a)*vy
d=(1-cos(a))*vy*vx+sin(a)*vz
e=cos(a)+(1-cos(a))*vy*vy
f=(1-cos(a))*vy*vz-sin(a)*vx
g=(1-cos(a))*vz*vx-sin(a)*vy
h=(a-cos(a))*vz*vy+sin(a)*vx
i=cos(a)+(1-cos(a))*vz*vz
Получается уже не такая страшная матрица:
a, b, c, 0
d, e, f, 0
g, h, i, 0
0, 0, 0, 1
Чтобы повернуть любую точку (x,y,z), используя эту матрицу, достаточно перемножить координаты точки на матрицу, добавив еще единицу как четвертую координату.
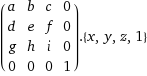
Перемножаем, получая новые координаты точки (x,y,z) (повернутые на заданный угол вокруг заданного вектора)
newx = a*x + b*y + c*z
newy = d*x + e*y + f*z
newz = g*x + h*y + i*z
Можете использовать эту формулу перемножения, вообще не думая о матрицах.
Просто подставляйте вместо букв a-i соответствующие куски тригонометрии, которые я выше написал.