Почему ближайшие точки определяются неправильно?

Question

[Quark]

Здравствуйте, появилась необходимость найти точку пересечения между двумя осями(помечены красной стрелкой на картинке)


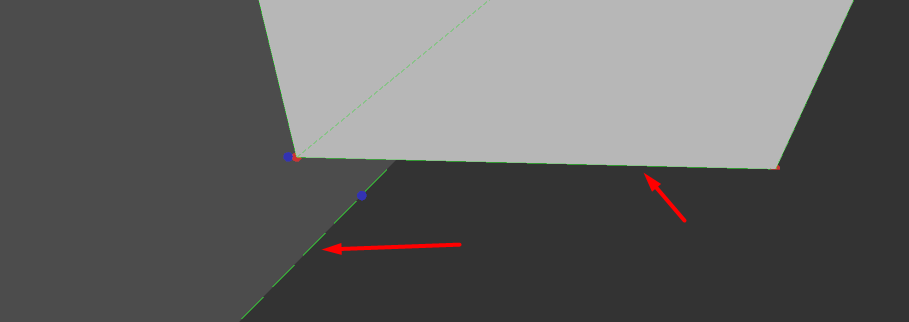
Так как оси эти, на самом деле, не пересекаются, а просто расположены очень близко друг к другу, то я предположил, что найдя ближайшую точку между ними, я смогу найти то, что мне нужно.

Однако мой код выдаёт странные ближайшие точки(помечены синим на скриншоте). Соответсвенно при их усреднении я получаю не то, что ожидал от алгоритма.

Вот мой код для опеределния ближайших точек, на данный момент:

static inline bool ClosetPointBetweenAxis(std::pair<Vector3, Vector3> axis1,std::pair<Vector3, Vector3> axis2, Vector3& point1, Vector3& point2) {
		Vector3 axis1Vector = axis1.second - axis1.first;
		Vector3 axis2Vector = axis2.second - axis2.first;

		Vector3 originVector = axis2.first - axis1.first;

		float normU = Vector3::DotProduct(Vector3::GetNormalize(axis1Vector), Vector3::GetNormalize(axis2Vector));

		//parallel
		if (fabs(normU) == 1)
			return false;

		float u = Vector3::DotProduct(axis1Vector, axis2Vector);

		float dir1Length = Vector3::GetNonSqrtMagnitude(axis1Vector);
		float dir2Length = Vector3::GetNonSqrtMagnitude(axis2Vector);

		float t1 = (
			originVector.X * axis1Vector.X +
			originVector.Y * axis1Vector.Y +
			originVector.Z * axis1Vector.Z -
			u * (
				originVector.X * axis1Vector.X +
				originVector.Y * axis1Vector.Y +
				originVector.Z * axis1Vector.Z)) /
			(dir1Length - u * dir2Length);

		float t2 = (t1 * u -
			originVector.X * axis2Vector.X -
			originVector.Y * axis2Vector.Y -
			originVector.Z * axis2Vector.Z) /
			dir2Length;

		Vector3 p1 = axis1.first + axis1Vector * t1;
		Vector3 p2 = axis2.first + axis2Vector * t2;

		point1 = p1;
		point2 = p2;

		return true;
	}

Где я ошибся в данном алгоритме?

Comments

[Wataru]

Формулы-то откуда взялись?

[Quark]

решил привлечь чат гпт к этому, так как у самого проблемы с алгоритмизацией школьных формул.

[Wataru]

Quark, ЧатЖПТ вам сгенерировал бред. Никогда не спрашивайте у чатжпт что-то по теме, в которой вы не эксперт. Он примерно в половине очевидных вопросов и почти во всех неочевидных генерирует случайные, но правдоподобно выглядящие галюцинации. Формулы вообще не правильные.

[Wataru]

Quark, Вообще, чат-жпт можно только философам пользоваться. Иногда филологам, чтобы написать сочинение на тему, где все ответы правильные. Во всех остальных областях получите красивый, но бесполезный ответ.

[Quark]

Wataru, а как тогда выглядит правильный ответ?

Answer 1

[Quark]

Для будущих поколений вот рабочая версия:

static inline bool ClosetPointBetweenAxis(std::pair<Vector3, Vector3> axis1,std::pair<Vector3, Vector3> axis2, Vector3& point) {
		Vector3 axis1Vector = Vector3::GetNormalize(axis1.second - axis1.first);
		Vector3 axis2Vector = Vector3::GetNormalize(axis2.second - axis2.first);

		float normU = Vector3::DotProduct(axis1Vector, axis2Vector);

		//parallel
		if (fabs(normU) == 1)
			return false;

		Vector3 cn = Vector3::GetNormalize(Vector3::CrossProduct(axis2Vector ,axis1Vector));
		Vector3 projection = axis1Vector * Vector3::DotProduct(axis2.first - axis1.first, axis1Vector);
		Vector3 rejection = axis2.first - axis1.first - axis1Vector * Vector3::DotProduct(axis2.first - axis1.first, axis1Vector) - cn * Vector3::DotProduct(axis2.first - axis1.first, cn);
		Vector3 closetApproach = axis2.first - axis2Vector * Vector3::GetMagnitude(rejection) / Vector3::DotProduct(axis2Vector, Vector3::GetNormalize(rejection));

		point = closetApproach;
		return true;
	}

взята отсюда

Answer 2

[Wataru]

Есть еще вот такое решение. Выводится так: задаем обе прямые параметрически (точка + t или u, помноженная на вектор вдоль прямой). Получаем выражение для квадрата расстояния между точками как функцию от t и u. Ищем ее минимум, приравняв к 0 частичные производные. Там получаются 2 линейных уравнения.

Vector3 a = axis2.first - axis1.first;
Vector3 v1 = axis1.second - axis1.first;
Vector3 v2 = axis2.second - axis2.first;
float v11 = Vector3::DotProduct(v1, v1);
float v12 = Vector3::DotProduct(v1, v2);
float v22 = Vector3::DotProduct(v2, v2);
float av1 = Vector3::DotProduct(a, v1);
float av2 = Vector3::DotProduct(a, v2);
// Решаем систему методом Крамера:
// t*v11-u*v12=av1
// t*v12-u*v22=av2
float d1 = -av1*v22+v12*av2;
float d2 = v11*av2-v22*av1;
float d = -v11*v22+v12*v12;
float t = d1/d;
float u = d2/d;
point1 = axis1.first + v1 * t;
point2 = axis2.first + v2 * u;