Добрый день.
Слушаю курс по дискретной математике и в задачнике очень часто встречаются задания вроде "Сколько можно составить слов длины n из русских букв, что в нем есть слово X?" или "Сколько можно составить слов длины n из русских букв, что в нем нет слова X?". Правильно ли я понимаю, что в первом случае задача сводится к нахождению всех размещений с повторением оставшихся
n - len(x) букв?
То есть, например, количество слов длины 11, содержащих подслово "привет":
Слово "привет" - длина 6
Ещё 5 символов могут быть перед "привет", либо 4 символа до и 1 после, 3 до – 2 после и т.д.
Получаем следующий результат:
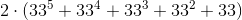
Верно ли я рассуждаю?