С помощью GLSL я пыталась нарисовать фрактал, который является визуализацией "группы Шоттки".
Опиралась на книгу "Indra's Pearls. The Vision of Felix Klein.", однако иллюстрации в ней отличаются от того, что выходит у меня.
Фрактал из книги:
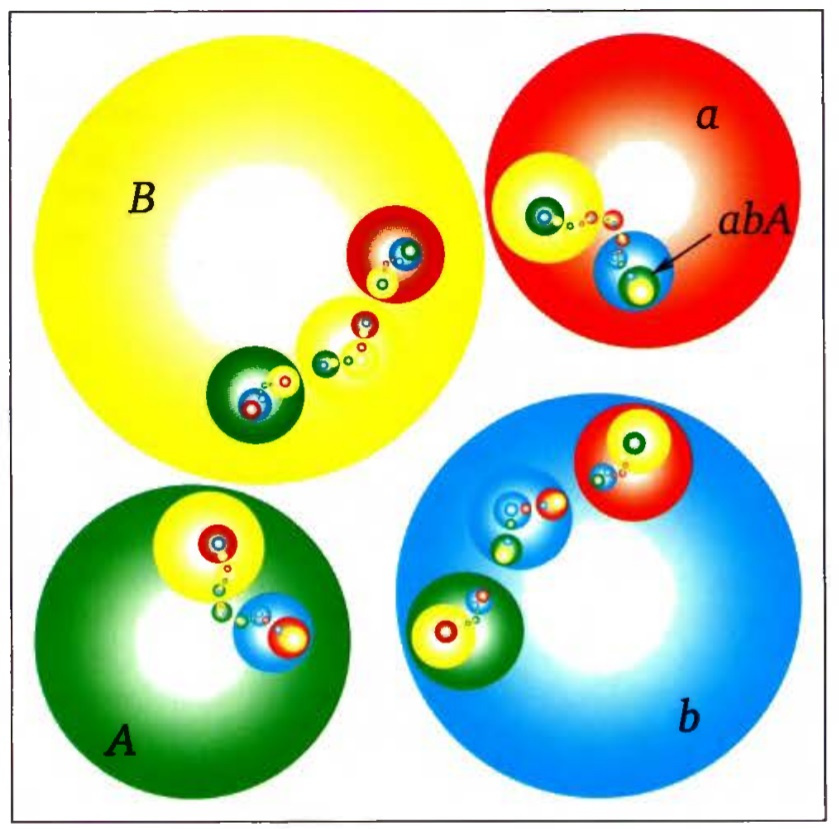
Мой фрактал:

Вот метод, который определяет преобразования Мёбиуса (основываясь на паре порождающих окружностей) и метод, определяющий яркость точки в зависимости от её координаты:
mobius connect(vec2 P, vec2 Q, float r, float s){
return normMobius(Q, one*r*s-zmz(P,Q), one, -P);
}
float DE(vec2 z){
vec2 O1 = vec2(-1.5,0.); float R1=1.;
vec2 O2 = vec2(1.5,0.); float R2=1.;
vec2 O3 = vec2(0.,-1.5); float R3=1.;
vec2 O4 = vec2(0.,1.5); float R4=1.;
mobius A = connect(O1,O2,R1,R2);
mobius a = connect(O2,O1,R2,R1);
mobius B = connect(O3,O4,R3,R4);
mobius b = connect(O4,O3,R4,R3);
int i=0,I=12;
for(;i<I;i++){
if(length(z-O1)<R1){
z=apply(A,z);
}else if(length(z-O2)<R2){
z=apply(a,z);
}else if(length(z-O3)<R3){
z=apply(B,z);
}else if(length(z-O4)<R4){
z=apply(b,z);
}else{
break;
}
}
return sqrt(float(i)/float(I));
}
Также, вот часть кода, которая описывает структуру преобразования Мёбиуса ( z -> (az+b)/(cz+d)).
struct mobius{
vec2 a,b,c,d;
};
mobius normMobius(vec2 a, vec2 b, vec2 c, vec2 d){
vec2 det = zmz(a,d)-zmz(b,c);
det = zpf(det,.5);
return mobius(zdz(a,det),zdz(b,det),zdz(c,det),zdz(d,det));
}
vec2 apply(mobius t, vec2 z){
return zdz(zmz(z,t.a)+t.b,zmz(z,t.c)+t.d);
}
Также, уточню, что zmz и zdz - умножение и деление комплексных чисел.
Итак, что я делаю не так? Почему такие преобразования порождают неправильный узор? Как их можно изменить?

