С точки зрения математика подобный цикл делается так: берём массив точек и идём по нему циклом, перебирая все рёбра. Аккумулятор угла инициализируем нулём. В каждой итерации цикла добавляем в аккумулятор арксинус угла между лучами из выбранной точки в вершины рёбер, знак которого зависит от направления поворота. По окончании цикла, если выяснилось, что в аккумуляторе ±2π, значит, точка внутри фигуры. Также, если одна из вершин точно совпала с точкой или если во время аккумуляции был скачок ±π (арксинус минус единицы), это значит, что точка на границе. Если точка снаружи, то аккумулятор как накопится, так и разрядится поворотами в противоположную сторону, и минус с плюсом уравновесятся.
С точки зрения программиста такую математику воплощать как есть рискованно. Вместо натурального логарифма программист по возможности возьмёт двоичный логарифм. И вместо проблемного арксинуса хочется взять что-то такое же по смыслу, но с меньшим накоплением ошибок. Я бы назвал это квадратный арксинус. Замеряет прогресс не по единичной окружности вокруг точки, а по единичному квадрату. На вход получает две пары координат, на выходе даёт число, которое в случае полного оборота накапливается не в ±2π, а в ±8.
Но для квадратичного арксинуса нужно выполнять снижающее точность деление, и накапливать продукты этого деления. Кажется, можно это оптимизировать ещё дальше, заменив вещественные числа дискретным номером октанта. В книгах по аналитической геометрии, наверное, лучше напишут.
Если требуют цикл, придётся разобраться хотя бы с арксинусами. А если нет, то условие принадлежности к границе в общем виде выглядит так:
if ((? = ?) and // строгое равенство для проверки принадлежности линии
(? <= ?) and (? >= ?)) or // два неравенства, чтоб линию обрезать с двух сторон и превратить в отрезок
// второй отрезок
((? = ?) and // строгое равенство для проверки принадлежности линии
(? <= ?) and (? >= ?)) or // два неравенства, чтоб линию обрезать с двух сторон и превратить в отрезок
// третий отрезок
// …
then
begin
// сообщить о том, что на границе
// …
Exit;
end; // if
Удобно сначала проверить принадлежность границе и выйти по Exit, а только потом проверять принадлежность толще.
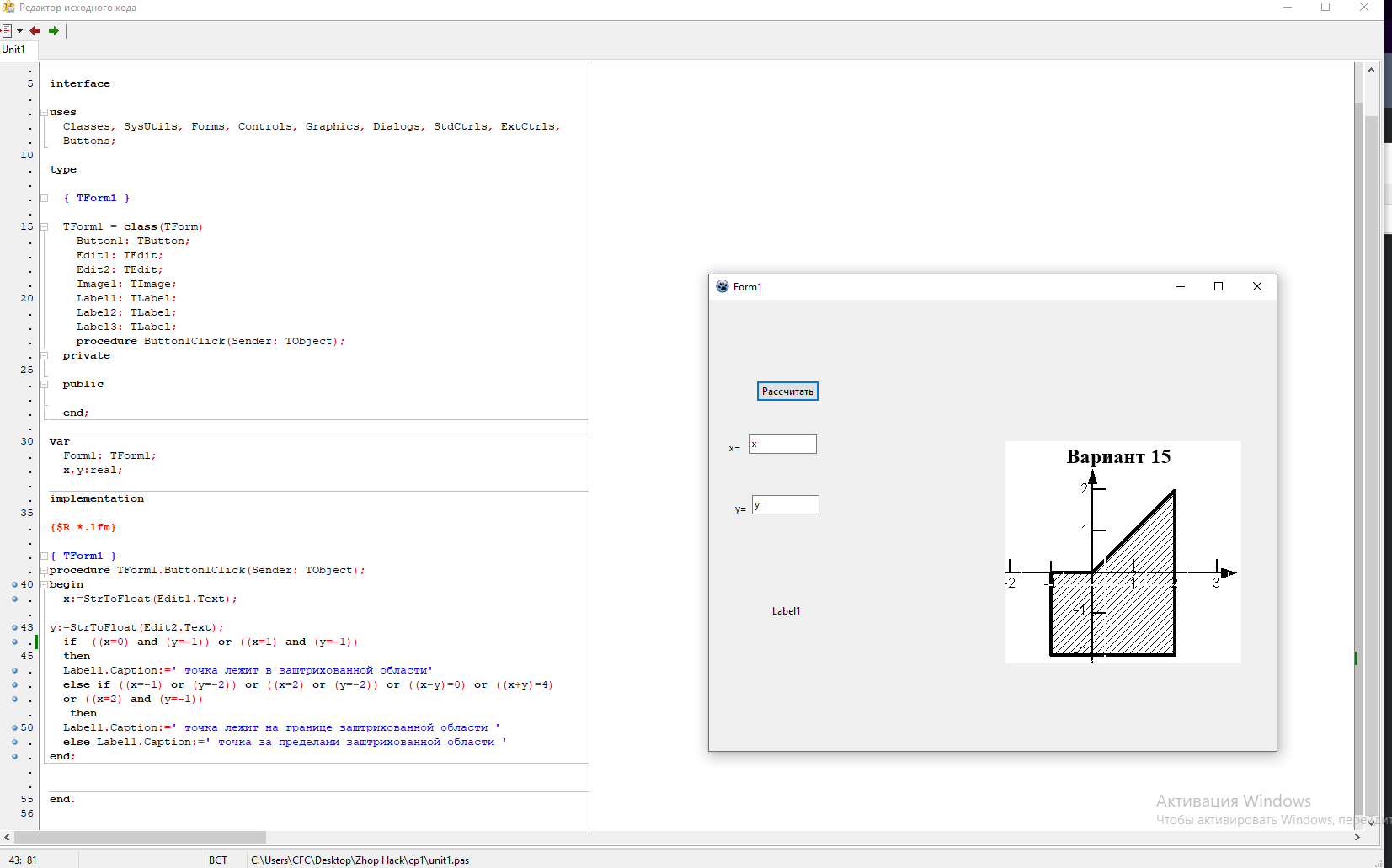
Вогнутый многоугольник в том виде, как на рисунке, очень удобно было бы деконструировать на два или более пересекающихся выпуклых многоугольника. Если принадлежит одному из выпуклых многоугольников, то принадлежит и искомому.
Принадлежность точки выпуклому многоугольнику определяется конъюнкцией неравенств для каждого ребра. Для выпуклого четырёхугольника:
(? <= ?) and (? <= ?) and (? <= ?) and (? <= ?)
Для треугольника:
(? <= ?) and (? <= ?) and (? <= ?)
Соединяем то и другое через or и получаем результат. Можно пойти и в другом направлении, не объединять множества точек, а вычитать. Глядя на рисунок, можно разглядеть объемлющий прямоугольник, из которого вычтена внутренность угла 135°. Внутренность угла можно задать двумя неравенствами
(? <= ?) and (? <= ?)
И объединить через and not:
(… внутри прямоугольника …) and not (… внутри угла …)